Introduction:
A branch of physics which provides a mathematical description of the dual particle-like and wave-like behavior and interactions of energy and matter is called Quantum mechanics (QM). It is also termed as quantum physics or quantum theory. It separates from classical mechanics primarily at the atomic and subatomic levels. The name was coined by Max Planck. As an example, the angular momentum of an electron bound into an atom is quantized. An electron bound in an atomic orbital have quantized values of angular momentum but an unbound electron does not have quantized energy levels. In the reference of QM, the wave–particle duality of energy and matter and the uncertainty principle provides view of the behavior of photons, electrons and other atomic-scale objects.
The mathematical calculations of quantum mechanics are abstract. The main part of the mathematical system is the wave function. The wave function is a mathematical function which can give information about the probable amplitude of position and momentum of a particle. The wave function emphasizes the object as a quantum harmonic oscillator.
The earliest versions of QM were formed in the first decade of the 20th century around the same time when the atomic theory and the corpuscular theory of light, updated by Einstein, first became accepted as scientific fact; these latter theories can be seen as "quantum theories" of matter and electromagnetic radiation. QM has undergone a significant re-formulation during mid -1920’s away from old quantum theory after the acceptance of the Copenhagen interpretation of Neil’s Bohr, Werner Heisenberg, Wolfgang Pauli and their associates. QM has been distributed into every aspect of 20th century physics and other disciplines such as quantum chemistry, quantum electronics, and quantum optics and quantum information science.
1) The behaviour of individual particles that make up all forms of matter—electrons, protons, neutrons, photons and others—can be satisfactorily explained by quantum mechanics.
2) It is important for understanding that how individual atoms combine covalently to form chemicals or molecules. This application of quantum mechanics is known as quantum chemistry.
3) A mechanism of a working of resonant tunnelling diode device is based on the phenomenon of quantum tunnelling by the potential barriers. Examples are the laser, the electron microscope, and magnetic resonance imaging.
4) A research topic is quantum teleportation which deals with techniques for transmitting quantum information over arbitrary distances.
5) QM applies to the atomic regimes of matter and energy, but some systems exhibit quantum mechanical effects on a large scale; Super fluidity is the best example.
In 1925, S.A. Goutsmit and G.E. Uhlenbeck suggested that an electron has an intrinsic angular momentum i.e. magnetic moment which is known as spin. In atomic physics, intrinsic angular momentum of given particle is parametrized by spin quantum number. Spin quantum number is of 4th number. The other three are principal quantum number, azimuthal quantum number and magnetic quantum number. The spin quantum number explains the unique quantum state of an electron. This is nominated as‘s’.
Spin quantum number holds that
Where
s is quantized spin vector,||s|| is the norm of the spin vector,
s is spin quantum number that is connected with the spin angular momentum, and h is Planck constant.
Analogous to orbital angular momentum(L), the spin vector (S) is quantized both in magnitude & direction and can be precised by spin quantum number s.
There are two orientations: 2 = 2s + 1 thus s = ½
The component Sz along z axis:
Sz = msh
ms = + ½ (spin up)
ms = -1/2 (spin down)
It is established that the intrinsic magnetic moment (μs) and angular momentum (S) vectors are proportional to each other:
Where gs is called gyromagnetic ratio. For the electron, the value of this g is 2.0023.
The properties of ‘electron spin’ were first explained by Dirac (1928), by combining the quantum mechanics with the theory of relativity.
If the atoms have even number of electrons then in each orbital, spin of each electron has differing orientation to that of its close neighbor(s). Though, some of the atoms have electrons in odd number or an composition of electrons in which there is an uneven number of ‘spin up’ and ‘spin down’ orientations. These type of electrons and atoms are known to have unpaired spins that are detected in electron spin resonance.
Classical mechanics, based on Newton's law of motion, successfully describes the motion of all macroscopic objects such as orbiting planets etc. which have essentially a particle like behaviour. However, it fails when applied to microscopic objects like electrons, atoms, molecules etc. This is due to the fact hat classical mechanics ignores the concept of dual behaviour of matter especially for subatomic particles and the uncertainty behaviour. The branch of science that takes into account this dual behaviour of matter is called quantum mechanics.
Quantum mechanics is a theoretical science that deals with the study of the motion of the microscopic objects that have both observable wave like and particle like properties. This science was developed independently by Werner Heisenberg and Erwin schrodinger. The direct and most important consequence of Heisenberg's uncertainty principle is its inability to determine the exact position of an electron in an atom when the energy of an electron is fixed and vice versa. Hence, we can only predict the probability of finding an electron in space around the nucleus and not its exact position.
The wave equation developed by Erwin Schrodinger provides a satisfactory description of an electron in an atom in these terms. Schrodinger won Nobel prize in physics in 1933 for this contribution to science. This wave equation formed the basis for the modern quantum mechanical model of the atom. The theory explains the dynamical properties of the microscopic particles in motion with high speed in terms of the wave nature of the particles. The most general form of the schrodinger's equation is given as :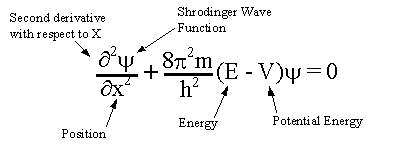
where m = mass of the electron
E = total energy of the electron (kinetic energy + potential energy)
v = potential energy of the electron
h = planck's constant
psi = Pronounced as 'Si' = wave function.
The equation applies to stationary waves as it does not have the time dependence part of the wave function.
1. The energy of electrons in an atom is quantize (it can only have certain specific values).
2. The existence of quantized electronic energy leaves is a direct result of the wave like properties of electrons and are allowed solution of schrodinger wave equation.
3. All the information about the electron in an atom is contained in its orbital wave function '`psi`' and quantum mechanics makes it possible to extract this information from 'psi`'.
4. The path of the electron can never be determined accurately. Therefore, we find only the probability of the electron at different points in space around an atom.
5. The probability of finding an electron at a point within an atom is proportional to the square of the orbital wave function i.e., |`psi`|2 at that point. |`psi`|2 is known as probability density and is always positive. From the value of |psi|2 at different points within the atom, it is possible to predict the region around the nucleus where electron will most probably be found.
Homework Assignment Help is World No 1 Online Assignment Help Company
@2010 - Copyright © All rights reserved | This is made with by Homework Assignment Help self
In case you face any problem or have any query please email us at :- info[@]homeworkassignmenthelp.com
Submit us an Assignment:
For Demo Class Click hereRead more
Our tutors start working only after the payment is made, to ensure that we are doing work only for serious clients and also our solution meets the required standard.
Getting homework help was never so easy you just need to follow following steps:
(for example: EST, Australian GMT etc)
any example or format you want the solutions to be in.
send you the price quoted by our tutor along with the time needed to solve the assignment
In case you face any problem or have any query please email us at :- info[@]homeworkassignmenthelp.com