Radioactive decay is the process by which an atomic nucleus of an unstable atom loses energy by emitting ionizing particles (ionizing radiation). The emission is spontaneous, in that the atom decays without any interaction with another particle from outside the atom (i.e., without a nuclear reaction). Usually, radioactive decay happens due to a proceses confined to the nucleus of the unstable atom, but occasonally (as with the different proceses of electron capture and internal conversion) an inner electron of the radioactive atom is also necessary to the process.
Introduction to radioactive decay physics
The scientist Fredric Soddy and Ernest Rutherford explained the radioactive decay physics. Fredric Soddy received the Nobel Prize in 1921 fro the radioactive decay and for the formulation of theory of isotopes. Radioactive decay is the result of an atom trying to achieve the stable configuration. In the radioactive decay process always can participate in the reaction and hence the reaction is nuclear.
The laws for the radioactive decay physics given by the famous scientists Rutherford and Fredrick Soddy. They both studied the radioactive decay experimentally. The laws for the radioactive decay are as follows:
(i) Radioactive decay phenomenon is a spontaneous process. Radioactive decay process does not depend on the external factors like temperature, pressure etc. It is impossible to guess that which on the particular atom will decay in the particular interval of time.
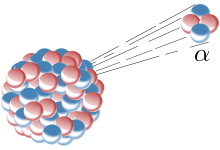
(ii) In the process of radioactive decay of an atom, either an alpha particle or a beta particle is emitted.No any two particles emitted simultaneously . Even no two alpha or beta particles simultaneously. At one time only one particle is emitted.
(iii) The emission of an alpha particle from an atom causes the decrement of two in atomic number and of four in mass number in the parent atom.
ZXA `->` Z–2 Y A – 4 + 2 He 4 (alpha particle)
(iv) The emission of a beta particle from an atom causes the increment in atomic number by one and the mass number remains same.
ZXA `->` Z+1 Y A + -1e 0 (beta particle)
(v) The number of atoms decayed per second at any instant is directly proportional to the number of atoms present in the sample at that instant. This law is also known as radioactive decay law.
Homework Assignment Help is World No 1 Online Assignment Help Company
@2010 - Copyright © All rights reserved | This is made with by Homework Assignment Help self
In case you face any problem or have any query please email us at :- info[@]homeworkassignmenthelp.com
Submit us an Assignment:
For Demo Class Click hereRead more
Our tutors start working only after the payment is made, to ensure that we are doing work only for serious clients and also our solution meets the required standard.
Getting homework help was never so easy you just need to follow following steps:
(for example: EST, Australian GMT etc)
any example or format you want the solutions to be in.
send you the price quoted by our tutor along with the time needed to solve the assignment
In case you face any problem or have any query please email us at :- info[@]homeworkassignmenthelp.com